Непозиционная система счисления пример, Непозиционная система счисления: что это такое и как она работает?

Позиционные системы счисления Двоичная система счисления Римская система счисления Системы счисления Другие заметки по информатике. Предшественница кириллической — с её помощью считали древние греки. В дальнейшем изложении будем рассматривать только позиционные системы. Дата обращения: 21 сентября
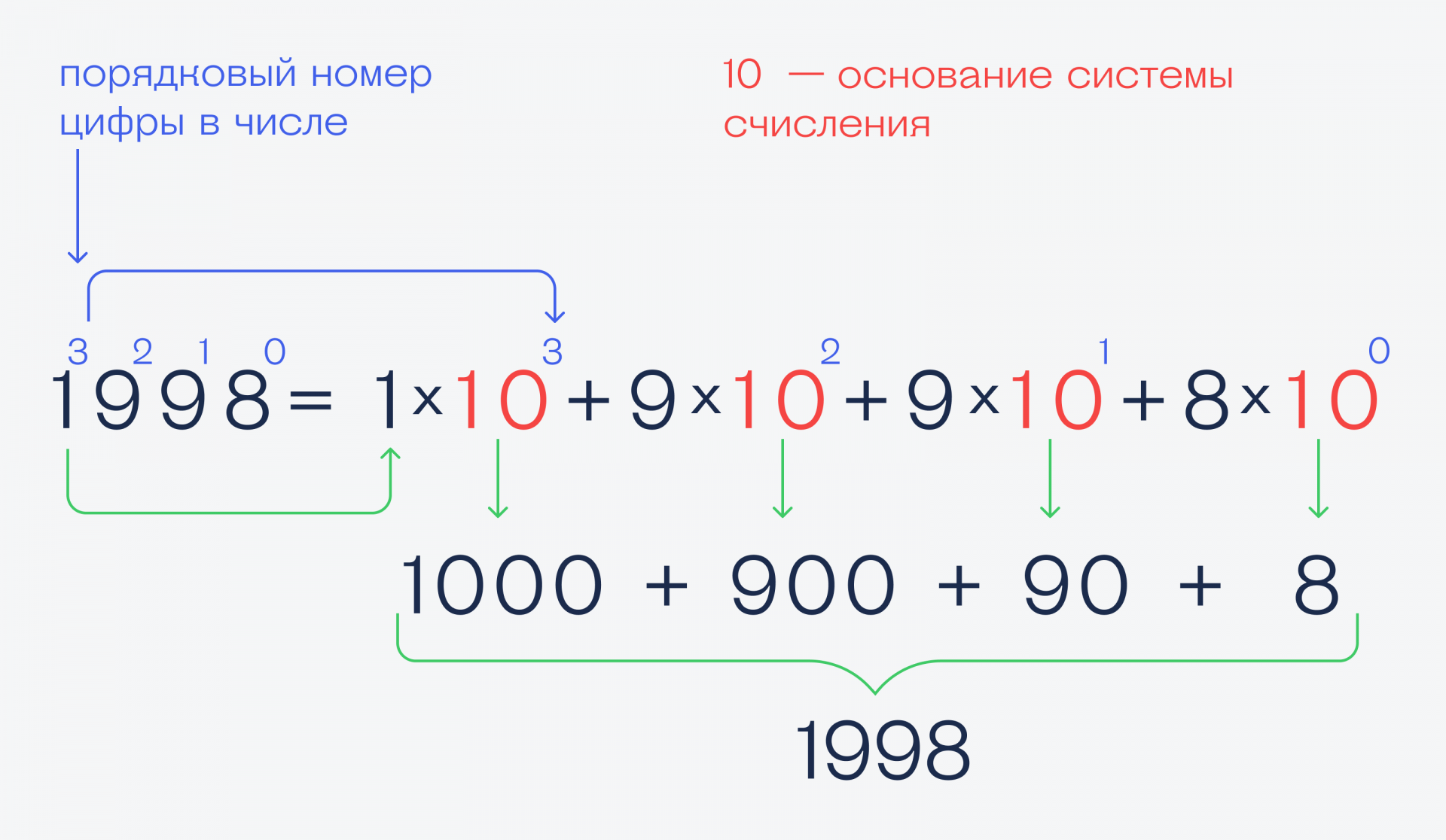
В основном, потому, что в повседневной жизни люди привыкли пользоваться десятичной системой счисления, и не требуется никакая другая. В вычислительных же машинах используется двоичная система счисления, так как оперировать числами, записанными в двоичном виде, довольно просто. Часто в информатике используют шестнадцатеричную систему, так как запись чисел в ней значительно короче записи чисел в двоичной системе.
Может возникнуть вопрос: почему бы не использовать для записи очень больших чисел систему счисления, например по основанию 50? Для такой системы счисления необходимы 10 обычных цифр плюс 40 знаков, которые соответствовали бы числам от 10 до 49 и вряд ли кому-нибудь понравится работать с этими сорока знаками. Поэтому в реальной жизни системы счисления по основанию, большему 16, практически не используются. Непозиционные системы счисления.
Как только люди начали считать, у них появилась потребность в записи чисел.

Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков бирок : зарубок, черточек, точек. Позже, для облегчения счета, эти значки стали группировать по три или по пять. Такая система записи чисел называется единичной унарной , так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Отголоски единичной системы счисления встречаются и сегодня.
Так, чтобы узнать, на каком курсе учится курсант военного училища, нужно сосчитать, какое количество полосок нашито на его рукаве. Сами того не осознавая, единичной системой счисления пользуются малыши, показывая на пальцах свой возраст, а счетные палочки используется для обучения учеников 1-го класса счету. Единичная система — не самый удобный способ записи чисел.
Записывать таким образом большие количества утомительно, да и сами записи при этом получаются очень длинными. С течением времени возникли иные, более удобные, системы счисления. Древнеегипетская десятичная непозиционная система счисления. Примерно в третьем тысячелетии до нашей эры древние египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, и т.
Все остальные числа составлялись из этих ключевых при помощи операции сложения. Система счисления Древнего Египта является десятичной, но непозиционной.
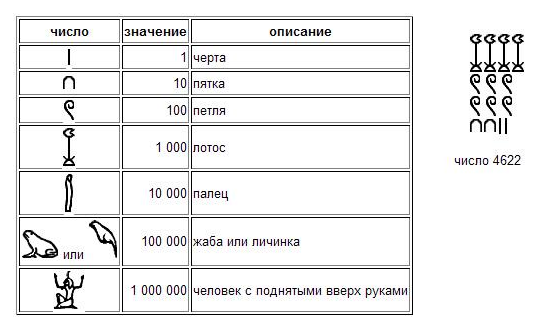
В непозиционных системах счисления количественный эквивалент каждой цифры не зависит от ее положения места, позиции в записи числа. Например, чтобы изобразить рисовали три цветка лотоса три тысячи , два свернутых пальмовых листа две сотни , пять дуг пять десятков и два шеста две единицы.
Величина числа не зависела от того, в каком порядке располагались составляющие его знаки: их можно было записывать сверху вниз, справа налево или вперемежку.
Римская система счисления. Примером непозиционной системы, которая сохранилась до наших дней, может служить система счисления, которая применялась более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежали знаки I один палец для числа 1, V раскрытая ладонь для числа 5, X две сложенные ладони для 10, а для обозначения чисел , и стали применять первые буквы соответствующих латинских слов Сentum — сто, Demimille — половина тысячи, Мille — тысяча.
Чтобы записать число, римляне разлагали его на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятков, единиц. Для записи промежуточных чисел римляне использовали не только сложение, но и вычитание. При этом применялось следующее правило: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него. Например, IX — обозначает 9, XI — обозначает Римскими цифрами пользовались очень долго. Еще лет назад в деловых бумагах числа должны были обозначаться римскими цифрами считалось, что обычные арабские цифры легко подделать.
Римская система счисления сегодня используется, в основном, для наименования знаменательных дат, томов, разделов и глав в книгах. Алфавитные системы счисления. Более совершенными непозиционными системами счисления были алфавитные системы.
К числу таких систем счисления относились греческая, славянская, финикийская и другие.
В них числа от 1 до 9, целые количества десятков от 10 до 90 и целые количества сотен от до обозначались буквами алфавита. В алфавитной системе счисления Древней Греции числа 1, 2, Для обозначения чисел 10, 20, Например, число обозначалось rma. При Петре I возобладала так называемая арабская нумерация, которой мы пользуемся и сейчас. Славянская нумерация сохранилась только в богослужебных книгах.
Непозиционные системы счисления имеют ряд существенных недостатков: 1. Существует постоянная потребность введения новых знаков для записи больших чисел. Невозможно представлять дробные и отрицательные числа.
Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения.
В ней используется всего лишь один знак — им могло быть все что угодно. В основном использовали палочки и камушки. К достоинствам можно отнести их простоту и небольшую сложность при выполнении арифметических операций с небольшими значениями. Вот вы и познакомились с непозиционными системами исчисления и можете легко про них рассказать. В связи с соотношением достоинств к недостаткам данных систем они были почти полностью вытесненными более совершенными позиционными исчислениями.
Фролова М. Непозиционные системы счисления В основе таких наук, как математика и информатика, огромную роль играют системы счисления.

Что такое непозиционные системы исчисления? К ним относятся: Римская система счисления Здесь в качестве алфавита для обозначения цифр используются латинские буквы. Славянская система счисления Нумерация, построенная на буквах кириллического и глаголического алфавита. Греческая Предшественница кириллической — с её помощью считали древние греки. Унарная Она же еще и единичная.
Достоинства непозиционных систем К достоинствам можно отнести их простоту и небольшую сложность при выполнении арифметических операций с небольшими значениями. Недостатки Отсутствие нуля, который играет огромную роль в точных науках.
Нет представления дробных величин. Сложность в выполнении умножения и деления. Для выполнения этих операций использовались большие таблицы. Для записи больших величин требовался ввод все новых и новых знаков, что являлось крайне неудобным. Сложность при переводе из одной такой системы в другую, так как они не были подчинены единому своду правил. Заключение Вот вы и познакомились с непозиционными системами исчисления и можете легко про них рассказать.